Más funciones para el análisis de datos geoestadístico según el libro"Model-based Geostatistics" de Peter J. Diggle & Paulo Justiniano Ribeiro Jr, 2007.
Iré agregando material teórico y práctico sobre el tema.
Book data set: http://www.leg.ufpr.br/doku.php/pessoais:paulojus:mbgbook:datasets
Iré agregando material teórico y práctico sobre el tema.
Book data set: http://www.leg.ufpr.br/doku.php/pessoais:paulojus:mbgbook:datasets
############################################################## #### Diggle Model Based Geoestadistics. Paquete geoR en R #### ############################################################## library(geoR)
data(elevation)
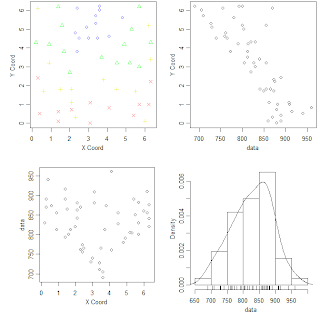
###2.8 perspectiva general de modelos geoestadísiticos: #análisis exploratorio no-espacialplot(elevation)
with(elevation, hist(data, main = "", xlab = "elevation")) with(elevation, plot(coords[, 1], data, xlab = "W-E", ylab = "elevation data", pch = 20, cex = 0.7)) lines(lowess(elevation$data ~ elevation$coords[, 1])) with(elevation, plot(coords[, 2], data, xlab = "S-N", ylab = "elevation data", pch = 20, cex = 0.7)) lines(with(elevation, lowess(data ~ coords[, 2]))) #modelo lineal con covariables. The values "1st" and "2nd" passed to the argument trend are aliases to indicate first-degree and second-degree polynomials on the coordinates. points(elevation, cex.max = 2.5) points(elevation, trend = "1st", pt.div = 2, abs = T, cex.max = 2.5) points(elevation, trend = "2nd", pt.div = 2, abs = T, cex.max = 2.5)
#calculo de los variogramas empíricos para los datos y los residuales
plot(variog(elevation, uvec = seq(0, 5, by = 0.5)), type = "b") res1.v <- variog(elevation, trend = "1st", uvec = seq(0, 5, by = 0.5)) plot(res1.v, type = "b") res2.v <- variog(elevation, trend = "2nd", uvec = seq(0, 5, by = 0.5)) lines(res2.v, type = "b", lty = 2) #variograma residual y envolventes de simulación bajo permutación aleatoria de los residuales. set.seed(231) mc1 <- variog.mc.env(elevation, obj = res1.v) plot(res1.v, env = mc1, xlab = "u") mc2 <- variog.mc.env(elevation, obj = res2.v) plot(res2.v, env = mc2, xlab = "u")
#estimaciones por ML (maximum likelihood) del modelo Gaussiano sin y con el término de tendencia. ml0 <- likfit(elevation, ini = c(3000, 2), cov.model = "matern", kappa = 1.5); ml0 ml1 <- likfit(elevation, trend = "1st", ini = c(1300, 2), cov.model = "matern", kappa = 1.5); ml1 #interpolación espacial con kriging locs <- pred_grid(c(0, 6.3), c(0, 6.3), by = 0.1) KC <- krige.control(type = "sk", obj.mod = ml0) sk <- krige.conv(elevation, krige = KC, loc = locs) KCt <- krige.control(type = "sk", obj.mod = ml1, trend.d = "1st", trend.l = "1st") skt <- krige.conv(elevation, krige = KCt, loc = locs) #selección de funciones gráficas para producir mapas usando argumentos opcionales para asegurar que los pares usan la misma escala gris pred.lim <- range(c(sk$pred, skt$pred)) sd.lim <- range(sqrt(c(sk$kr, skt$kr))) image(sk, col = gray(seq(1, 0, l = 51)), zlim = pred.lim) contour(sk, add = T, nlev = 6) points(elevation, add = TRUE, cex.max = 2) image(skt, col = gray(seq(1, 0, l = 51)), zlim = pred.lim) contour(skt, add = T, nlev = 6) points(elevation, add = TRUE, cex.max = 2) image(sk, value = sqrt(sk$krige.var), col = gray(seq(1, 0, l = 51)), zlim = sd.lim) contour(sk, value = sqrt(sk$krige.var), levels = seq(10, 27, by = 2), add = T) points(elevation$coords, pch = "+") image(skt, value = sqrt(skt$krige.var), col = gray(seq(1, 0, l = 51)), zlim = sd.lim) contour(skt, value = sqrt(skt$krige.var), levels = seq(10, 27, by = 2), add = T) points(elevation$coords, pch = "+")
#dejar fuera el efecto de la covariable: remoción de tendencia
### 3.13 Modelos Gaussianos para datos geoestadísticos #cálculo y gráfico de la función de correlación estándar. Se elige la familia de correlaciones con el argumento cov.model. x <- seq(0, 1, l = 101) plot(x, cov.spatial(x, cov.model = "mat", kappa = 0.5, cov.pars = c(1, 0.25)), type = "l", xlabel = "u", ylabel = expression(rho(u)), ylim = c(0, 1)) lines(x, cov.spatial(x, cov.model = "mat", kappa = 1.5, cov.pars = c(1, 0.16)), lty = 2) lines(x, cov.spatial(x, cov.model = "mat", kappa = 2.5, cov.pars = c(1, 0.13)), lty = 3)
#generar simulaciones de procesos Gaussianos 2D. La función grf() especifica el modelo y las localizaciones para lso valores simulados requeridos. set.seed(159) #asegura que las simulaciones se gneran con el mismo número aleatorio de semilla, y por tanto las realizaciones simuladas tienen diferencias solo por los valores diferentes de los parámetros del modelo. image(grf(100^2, grid = "reg", cov.pars = c(1, 0.25)), col = gray(seq(1, 0, l = 51)), xlab = "", ylab = "") set.seed(159) image(grf(100^2, grid = "reg", cov.pars = c(1, 0.13), cov.model = "mat", kappa = 2.5), col = gray(seq(1, 0, l = 51)), xlab = "", ylab = "") #simulaciones de modelos anisotrópicos set.seed(421) image(grf(201^2, grid = "reg", cov.pars = c(1, 0.25), aniso.pars = c(pi/3, 4)), col = gray(seq(1, 0, l = 51)), xlab = "", ylab = "") set.seed(421) image(grf(201^2, grid = "reg", cov.pars = c(1, 0.25), aniso.pars = c(3 * pi/4, 2)), col = gray(seq(1, 0, l = 51)), xlab = "", ylab = "")
#In this case, we have used a stationary Gaussian model with mean mu = 850, nugget variance tau^2 = 100, signal variance sigma^2 = 3500 and MatLern correlation function with k = 2.5 and phi= 0.8. sim1 <- grf(100, cov.pars = c(1, 0.15), cov.model = "matern", kappa = 1.5) points(sim1) data(elevation) sim2 <- grf(grid = elevation$coords, cov.pars = c(3500, 0.8), nugget = 100) sim2$data <- sim2$data + 850 points(sim2)
### 4.6 Modelos lineales generalizados (GLM) para datos geoestadísticos
#simulación con el GLM de un modelo de Poisson #simulate a realisation of the Gaussian process at these locations with mu= 0.5, sigma^2 = 2 and MatLern correlation function with k = 1.5, phi = 0.2. set.seed(371) cp <- expand.grid(seq(0, 1, l = 10), seq(0, 1, l = 10)) s <- grf(grid = cp, cov.pars = c(2, 0.2), cov.model = "mat", kappa = 1.5) image(s, col = gray(seq(1, 0.2, l = 21))) lambda <- exp(0.5 + s$data) y <- rpois(length(s$data), lambda = lambda) text(cp[, 1], cp[, 2], y, cex = 1.5) #extensión del modelo, incluyendo variación no-espacial extra de Poisson lambda <- exp(s$data + tau * rnorm(length(s$data))) #simulación con GLM del modelo Bernoulli set.seed(34) locs <- seq(0, 1, l = 401) s <- grf(grid = cbind(locs, 1), cov.pars = c(5, 0.1), cov.model = "matern", kappa = 1.5) p <- exp(s$data)/(1 + exp(s$data)) ind <- seq(1, 401, by = 8) y <- rbinom(p[ind], size = 1, prob = p) plot(locs[ind], y, xlab = "locations", ylab = "data") lines(locs, p)
#simulación con GLM del modelo Binomial. Con [Y (x)|S] ¡« Bin{n, p(x)} with n = 5 and p(x) = exp{mu + S(x)}/[1 + exp{mu + S(x)}], set.seed(23) s <- grf(60, cov.pars = c(5, 0.25)) p <- exp(2 + s$data)/(1 + exp(2 + s$data)) y <- rbinom(length(p), size = 5, prob = p) points(s) text(s$coords, label = y, pos = 3, offset = 0.3)
### Estimación de parámetros clásica: estimaciónd e tendencia, variogramas, estimación de la estructura de covarianza (OLS, WLS, etc), ML, estimación paramétrica por modelos lineales generalizados, MCML, etc. #calculo de variograma con diferentes opciones del tamaño bin data(elevation) plot(variog(elevation, option = "cloud"), xlab = "u", ylab = "V(u)") plot(variog(elevation, uvec = seq(0, 8, by = 0.5)), xlab = "u", ylab = "V(u)") plot(variog(elevation, trend = "2nd", max.dist = 6.5), xlab = "u", ylab = "V(u)")
data(s100) #datos simulados con un modelo con media=cero, varianza=uno, nugget=0, y función de correlación exponencial con phi=.3. v1 <- variog(s100); plot(v1) v2 <- variog(s100, uvec = seq(0, 1, by = 0.1)); plot(v2) v3 <- variog(s100, max.dist = 1); plot(v3) round(v1$u, dig = 2) #The midpoints of the bins obtained from the commands listed above round(v2$u, dig = 2) round(v3$u, dig = 2)
data(ca20) plot(ca20,trend= area+altitude, low=T) #sugiere tendencia cuadratica plot(variog(ca20, max.dist = 510)) #construimos distintos variogramas: observamos que incorporando sub-regoses al modelo este se comporta aproximadamente estacionario en los residuales plot(variog(ca20, trend = ~area, max.dist = 510)) plot(variog(ca20, trend = ~area + altitude, max.dist = 510)) t.all <- trend.spatial(ca20, trend = ~area + altitude, add = "2nd") plot(variog(ca20, trend = ~t.all, max.dist = 510)) set.seed(83) #variogramas de las simulaciones del proceso Gaussiano, cada gráfico indica el variograma verdadero y la curva suavizada, así como los variogramas empíricos de las tres simulaciones del proceso en 100 localizaciones. sim1 <- grf(100, cov.pars = c(1, 0.05), cov.model = "mat", kap = 1.5, nsim = 3) #Parameter values are k 1.5, sigma^2= 1, tau^2 = 0 in both panels. In the left-hand panel, phi= 0.05, in the right-hand panel phi= 0.2. plot(variog(sim1, max.dist = 1), type = "l", lty = 1:3, col = 1) lines.variomodel(seq(0, 1, l = 100), cov.model = "mat", kap = 1.5, cov.pars = c(1, 0.05), nug = 0) set.seed(83) sim2 <- grf(100, cov.pars = c(1, 0.2), cov.model = "mat", kap = 1.5, nsim = 3) plot(variog(sim2, max.dist = 1), type = "l", lty = 1:3, col = 1) lines.variomodel(seq(0, 1, l = 100), cov.model = "mat", kap = 1.5, cov.pars = c(1, 0.2), nug = 0)#estimación de parámetros en modelos gaussianos con particular foco en los parámetros que definen la estructura de covarianza del modelo. s100.v <- variog(s100, max.dist = 1) #estimación mediante variograma plot(s100.v); lines.variomodel(seq(0, 1, l = 100), cov.pars = c(0.9, 0.2), cov.model = "mat", kap = 1.5, nug = 0.2)
wls <- variofit(s100.v, ini = c(0.9, 0.2), cov.model = "mat", kap = 1.5, nug = 0.2); wls #estimación mediante WLS ml <- likfit(s100, cov.model = "mat", kap = 1.5, ini = c(0.9, 0.2), nug = 0.2); ml #estimación por ML reml <- likfit(s100, cov.model = "mat", kap = 1.5, ini = c(0.9, 0.2), nug = 0.2, met = "reml"); reml #estimación por ML restringido #ajuste de 5 modelos alternaticos a los datos de suelo y sus covariables. data(ca20) m1 <- likfit(ca20, ini = c(100, 200), nug = 50) m2 <- likfit(ca20, trend = ~area, ini = c(60, 100), nug = 40) m3 <- likfit(ca20, trend = ~area + altitude, ini = c(60, 100), nug = 40) m4 <- likfit(ca20, trend = ~area + coords, ini = c(60, 100), nug = 40) m5 <- likfit(ca20, trend = ~area + altitude + coords, ini = c(60, 100), nug = 40) ### Predicción espacial #predicción por "conventional kriging" data(SIC) ml <- likfit(sic.all, ini = c(100, 40), nug = 10, lambda = 0.5, kappa = 1) #estimjación de los parámetros del modelo gr <- pred_grid(sic.borders, by = 7.5) #definimos una grilla para lso puntos de predicción KC <- krige.control(obj.model = ml) #pasa los parámetros del modelo mediante "ordinary krigning" OC <- output.control(n.pred = 1000, simul = TRUE, thres = 250) #incluye opciones para generar y guardar 1000 simulaciones de las distribuciones condicionales de S dado Y y definir un valor umbral de 250 que será usado para calcular la probabilidad de excedencia en cada localización de la predicción. set.seed(2419) #permite la reproducción de los resultados de la simulación pred <- krige.conv(sic.all, loc = gr, borders = sic.borders,krige = KC, out = OC) image(pred, col = gray(seq(1, 0.1, l = 21)), zlim = predlim, x.leg = c(0, 350), y.leg = c(-60, -30)) image(pred, loc = gr, val = sqrt(pred$krige.var), zlim = selim, col = gray(seq(1, 0.1, l = 21)), x.leg = c(0, 350), y.leg = c(-60, -30)) dim(pred$simulations) A200 <- apply(pred$simul, 2, function(y) sum(y > 200)/length(y)) hist(A200, main = "") image(pred, val = 1 - pred$prob, col = gray(seq(0.9, 0.1, l = 41)), x.leg = c(0, 350), y.leg = c(-60, -30))
#el mismo análisis para los datos de calcio en el suelo data(ca20) fit <- likfit(ca20, ini = c(100, 60), trend = ~area) gr <- pred_grid(ca20$borders, by = 10) gr0 <- polygrid(gr, borders = ca20$border, bound = T) ind.reg <- numeric(nrow(gr0)) ind.reg[.geoR_inout(gr0, ca20$reg1)] <- 1 ind.reg[.geoR_inout(gr0, ca20$reg2)] <- 2 ind.reg[.geoR_inout(gr0, ca20$reg3)] <- 3 ind.reg <- as.factor(ind.reg) KC <- krige.control(trend.d = ~area, trend.l = ~ind.reg, obj.model = fit) ca20pred <- krige.conv(ca20, loc = gr, krige = KC) par(mar = c(2.8, 2.5, 0.5, 0.5), mgp = c(1.8, 0.7, 0), mfrow = c(1, 2)) image(ca20pred, loc = gr, col = gray(seq(1, 0, l = 21)), x.leg = c(4930, 5350), y.leg = c(4790, 4840)) polygon(ca20$reg1) polygon(ca20$reg2) polygon(ca20$reg3) image(ca20pred, loc = gr, val = sqrt(ca20pred$krige.var), col = gray(seq(1, 0, l = 21)), x.leg = c(4930, 5350), y.leg = c(4790, 4840)) polygon(ca20$reg1) polygon(ca20$reg2) polygon(ca20$reg3) coords <- cbind(c(0.2, 0.25, 0.6, 0.7), c(0.1, 0.8, 0.9, 0.3)) KC <- krige.control(ty = "ok", cov.model = "mat", kap = 1.5, nug = 0.1, cov.pars = c(1, 0.1)) krweights(coords, c(0.5, 0.5), KC)















Comentarios
Publicar un comentario